Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
The Class 9 is an important year in a student’s life and Maharashtra State Board Maths 1 is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 9 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 9 Maths 1 Book syllabus.

Practice set 2.1 Page no: 21
1. Classify the decimal form of the given rational numbers into terminating and non-terminating recurring type.
i. 13/5
iv. 17/125
v. 11/6
Solution:
i.
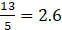
∵ The division is exact
∴ it is a terminating decimal.
ii.
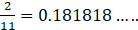
∵ The division never ends and the digits ‘18’ is repeated endlessly
∴ it is a non-terminating recurring type decimal.
iii.
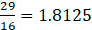
∵ The division is exact
∴ it is a terminating decimal.
iv.
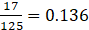
∵ The division is exact
∴ it is a terminating decimal.
v.
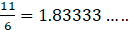
∵ The division never ends and the digit ‘3’ is repeated endlessly
∴ it is a non-terminating recurring type decimal.
2. Write the following rational numbers in decimal form.
i. 127/200
ii. 25/99
iii. 23/7
iv. 4/5
v. 17/8
Solution:
i.

ii.
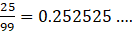
iii.
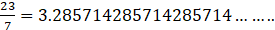
iv.

v.
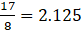
3. Write the following rational numbers in form.
i. 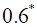
ii. 
iii. 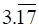
iv. 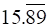
v. 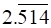
Solution:
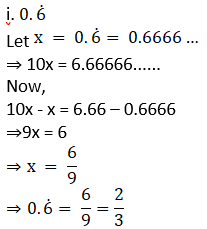



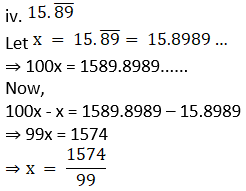
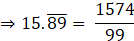

Practice set 2.2 Page no: 25
1. Show that is 4√2 an irrational number.
Solution:

2. Prove that 3 + √5 is an irrational number.
Solution:

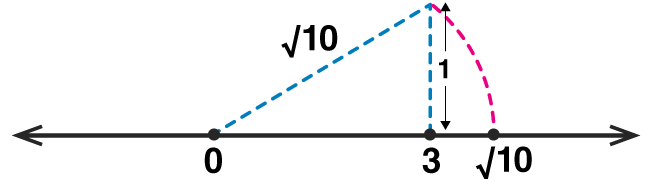
3. Represent the numbers √5 and √10 on a number line.
Solution:
Given √5


Given that √10

4. Write any three rational numbers between the two numbers given below.
(i) 0.3 and -0.5
Solution:


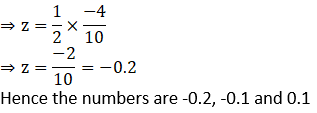
(ii) -2.3 and -2.33
Solution:


(iii) 5.2 and 5.3
Solution:


(iv) -4.5 and 4.6
Solution:


Practice set 2.3 Page no: 30
1. State the order of the surds given below.
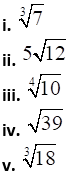
Solution:

2. State which of the following are surds. Justify.

Solution:

iv. √256 = √162 = 16
Surds are numbers left in root form (√) to express its exact value. It has an infinite number of non-recurring decimals. Therefore, surds are irrational numbers.
It is not a surd ∵ it is a rational number.

3. Classify the given pair of surds into like surds and unlike surds.
i. √52, 5√13
ii. √68, 5√3
iii. 4√18, 7√2
iv. 19√12, 6√3
v. 5√22, 7√33
vi. 5√5, √75
Solution:
Two or more surds are said to be similar or like surds if they have the same surd-factor.
Two or more surds are said to be dissimilar or unlike when they are not similar.
Therefore,
i. Given √52, 5√13
given surd can be written as
√52 = √ (2×2×13) = 2√13
5√13
∵ both surds have same surd-factor that is √13.
∴ they are like surds.
ii. Given √68, 5√3
Given surd can be written as
√68 = √ (2×2×17) = 2√17
5√3
∵ both surds have different surd-factors √17 and √3.
∴ they are unlike surds.
iii. Given 4√18, 7√2
Given surd can be written as
4√18 = 4 √ (2×3×3) = 4×3√2 = 12√2
7√2
∵ both surds have same surd-factor i.e., √2.
∴ they are like surds.
iv. Given 19√12, 6√3
Given surd can be written as
19√12 = 19√ (2×2×3) = 19×2√3 = 38√3
6√3
∵ both surds have same surd-factor i.e., √3.
∴ they are like surds.
v. Given 5√22, 7√33
∵ both surds have different surd-factors √22 and √33.
∴ they are unlike surds.
vi. Given 5√5, √75
5√5
Given surd can be written as
√75 = √ (5×5×3) = 5√3
∵ both surds have different surd-factors √5 and √3.
∴ they are unlike surds.
4. Simplify the following surds.
i. √27
ii. √50
iii. √250
iv. √112
v. √168
Solution:

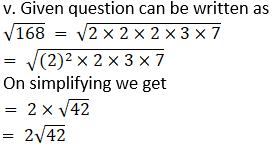
Practice set 2.4 Page no: 32
1. Multiply
i. √3(√7 – √3)
ii. (√5 – √7) √2
iii. (3√2 – √3) (4√3 – √2)
Solution:
i. Given √3 (√7 – √3)
=√3 × √7 – √3 × √3
[∵ √a (√b – √c) = √a × √b – √a × √c]=√21 – 3
ii. Given (√5 – √7) √2
=√5 × √2 – √7 × √2
[∵√a (√b – √c) = √a × √b – √a × √c]= √10 – √14
iii. Given (3√2 – √3) (4√3 – √2)
=3√2 (4√3 – √2) – √3 (4√3 – √2)
[∵ √a (√b – √c) = √a × √b – √a × √c]= 3√2 × 4√3 – 3√2 × √2 – √3 × 4√3 + √3 × √2
= 12√6 – 3 × 2 – 4 × 3 + √6
= 12√6 – 6 – 12 + √6
= 13√6 – 18
2. Rationalize the denominator.
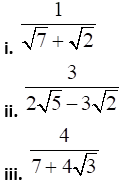
iv. 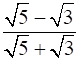
Solution:
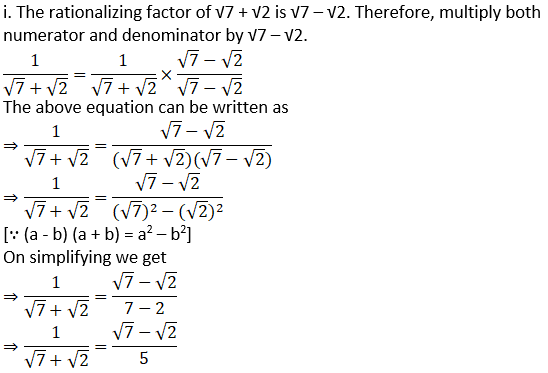
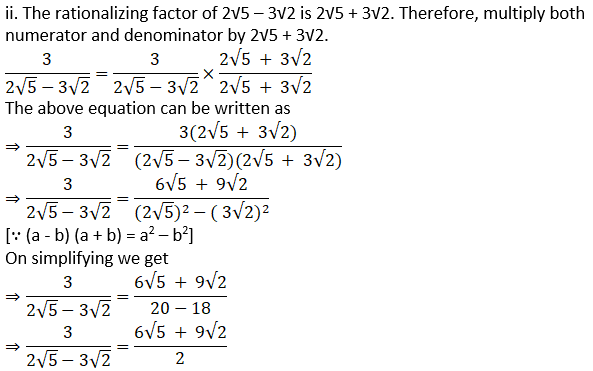



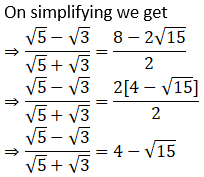
Practice set 2.5 Page no: 33
1. Find the value.
(i) |15 –2|
(ii) |4 –9|
(iii) |7| × |-4|
Solution:
i. Given |15 –2|
Absolute value describes the distance of a number on the number line from 0 without considering which direction from zero the number lies. The absolute value of a number is never negative.
Therefore,
|15 –2| = |13| = 13
ii. Given |4 –9|
Absolute value describes the distance of a number on the number line from 0 without considering which direction from zero the number lies. The absolute value of a number is never negative.
Therefore,
|4 –9| = |-5| = 5
iii. Given |7| × |-4|
Absolute value describes the distance of a number on the number line from 0 without considering which direction from zero the number lies. The absolute value of a number is never negative.
Therefore,
|7| × |-4| = 7 × 4 = 28
2. Solve.
i. |3x –5| = 1
ii. |7 – 2x| = 5
iii. 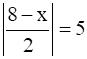
iv. 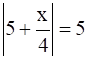
Solution:
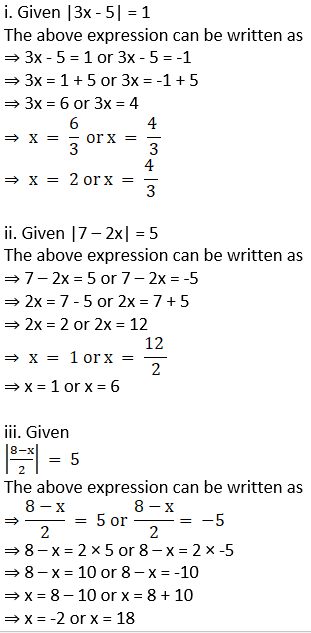
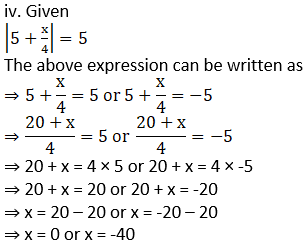

Problem set 2 Page no: 34
1. Choose the correct alternative answer for the questions given below.
i. Which one of the following is an irrational number?
A. √16/25
B. √5
C. 3/9
D. √196
Solution:
B. √5
Explanation:
An irrational number is a number that cannot be expressed as a fraction p/q for any integers p and q and q ≠ 0.
Since √5 cannot be written as p/q it is an irrational number
Therefore √5 is an irrational number.
ii. Which of the following is an irrational number?
A. 0.17
B. 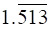
C. 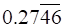
D. 0.101001000 ….
Solution:
D. 0.101001000 ….
Explanation:
An irrational number is a number that cannot be expressed as a fraction p/q for any integers p and q and q ≠ 0.
0.101001000 …. is an irrational number because it is a non-terminating and non-`repeating decimal.
Therefore, 0.101001000 …. is an irrational number.
iii. Decimal expansion of which of the following is non-terminating recurring?
A. 2/5
B. 3/16
C. 3/11
D. 137/25
Solution:
C. 3/11
Explanation:
A non-terminating recurring decimal representation means that the number will have an infinite number of digits to the right of the decimal point and those digits will repeat themselves.
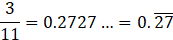
∵ it has an infinite number of digits to the right of the decimal point which are repeating themselves ∴ it is a non-terminating recurring decimal.
iv. Every point on the number line represent, which of the following numbers?
A. Natural numbers
B. Irrational numbers
C. Rational numbers
D. Real numbers.
Solution:
D. Real numbers.
Explanation:
Every point of a number line is assumed to correspond to a real number, and every real number to a point. Therefore, every point on the number line represent a real number.
v. The number 0.4 in p/q form is ………….
A. 4/9
B. 40/9
C. 3.6/9
D. 36/9
Solution:
C. 3.6/9
Explanation:

vi. What is √n, if n is not a perfect square number?
A. Natural number
B. Rational number
C. Irrational number
D. Options A, B, C all are correct.
Solution:
C. Irrational number
Explanation:
If n is not a perfect square number, then √n cannot be expressed as ratio of a and b where a and b are integers and b ≠ 0
Therefore, √n is an Irrational number
vii. Which of the following is not a surd?
A. √7
B. 3√17
C. 3√64
D. √193
Solution:
C. 3√64
Explanation:
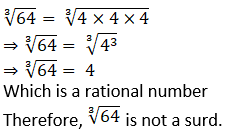
viii. What is the order of the surd 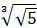 ?
?
A. 3
B. 2
C. 6
D. 5
Solution:
C. 6
Explanation:
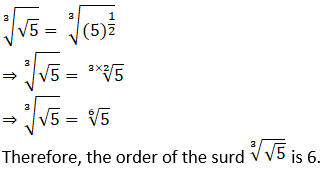
ix. Which one is the conjugate pair of 2√5 + √3?
A. -2√5 + √3
B. -2√5 –√3
C. 2√3 + √5
D. √3 + 2√5
Solution:
A. -2√5 + √3
Explanation:
A math conjugate is formed by changing the sign between two terms in a binomial. For instance, the conjugate of x + y is x –y.
Now,
2√5 + √3 = √3 + 2√5
Its conjugate pair = √3 –2√5 = -2√5 + √3
∴ The conjugate pair of 2√5 + √3 = -2√5 + √3
x. The value of |12 – (13 + 7) × 4| is ………..
A. -68
B. 68
C. -32
D. 32
Solution:
B. 68
Explanation:
|12 – (13 + 7) × 4| = |12 – 20 × 4|
(Solving it according to BODMAS)
⇒ |12 – (13 + 7) × 4| = |12 – 80|
⇒ |12 – (13 + 7) × 4| = |-68|
⇒ |12 – (13 + 7) × 4| = 68